Graph(그래프) :
그래프는 연결관계를 표현할 수 있는 자료구조이다.
예를 들어 사회 연결망, 위치 데이터 등을 그래프를 통해 나타낼 수 있다.
페이스북 및 SNS에서 팔로우 등의 연결관계, 구글 맵과 같은 지도, 지하철 노선도에서 최단경로, 구글을 통해 웹페이지를 검색할 때 하이퍼링크를 통해 다른 사이트와 연결된 관계 등 다양한 연결관계를 그래프로 표현할 수 있다.
그럼 그래프를 그림으로 보면서 이해해보자!

* Vertex(Node, 정점),
* Edge(간선): 노드를 연결하는 선
* Degree(차수): 하나의 노드에 연결된 간선들의 수
* 방향그래프 => in-degree(진입 차수): 외부에서 오는 간선의 수, out-degree(진출 차수): 외부로 향하는 간선의 수
* 경로 길이: 경로를 구성하는 데 사용된 간선의 수
그래프의 종류도 다양한데 위에서 보듯 '무방향 그래프(Undirected Graph)'와 '방향 그래프(Directed Graph)'로 나눌 수 있고,
그래프의 간선에 가중치(Wight)가 있는 '가중 그래프(Weighted Graph)'와 가중치가 없는 '균일 그래프(unweighted graph)'로 나눌 수도 있다. 가중 그래프는 아래와 같다.
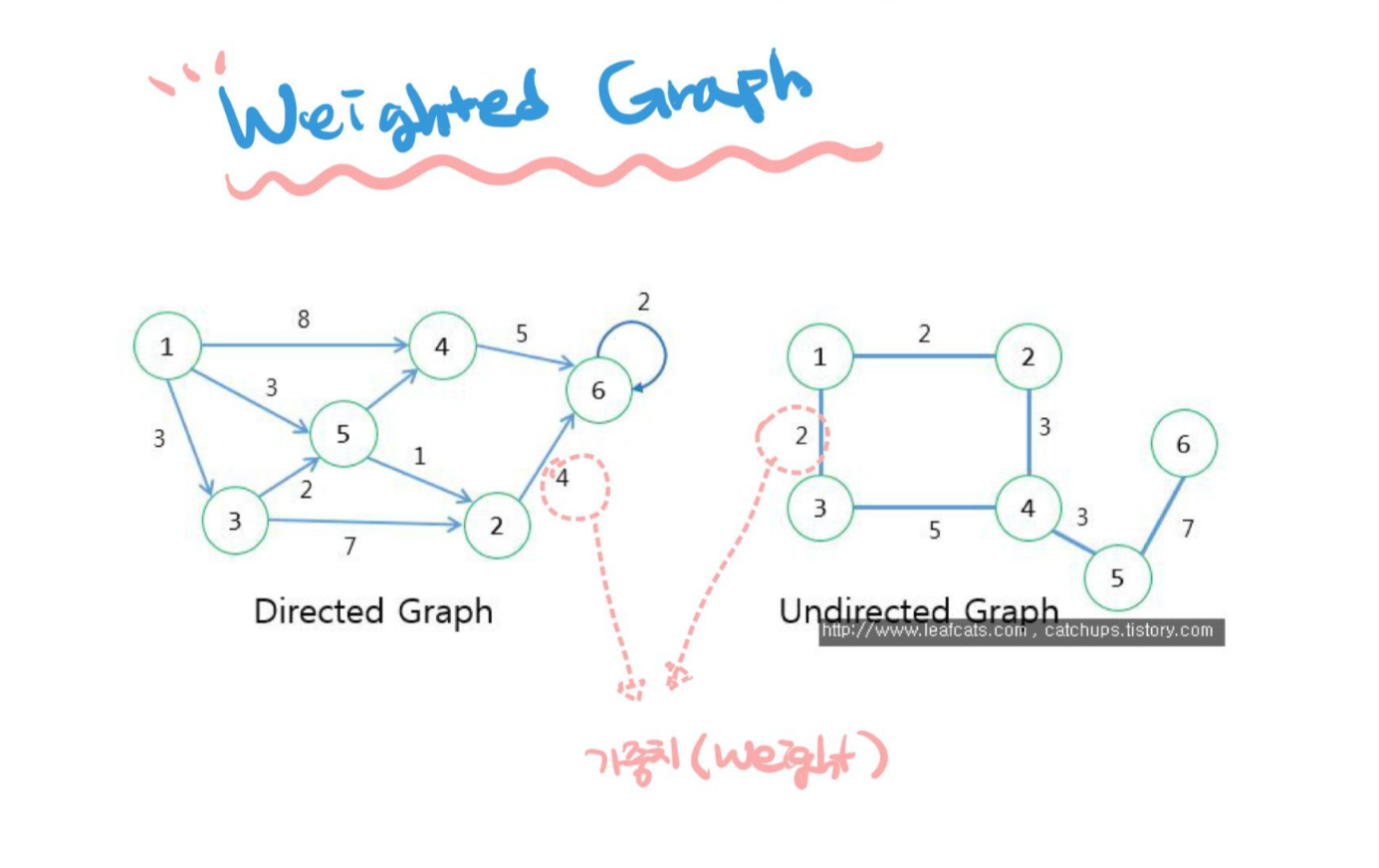
가중 그래프에서 경로의 거리 개념이 모든 간선의 가중치의 합이 된다. 그래서 최단 경로를 알고 싶으면 두 정점 간의 모든 경로에서 간선의 가중치 합이 최소가 되는 경로를 찾으면 된다!
그래프를 코드로 표현하는 방법은 크게 두 가지가 있다.
이차원 배열을 사용하는 인접 행렬 방식과 연결 리스트를 사용하는 인접 리스트 방식이 있다.
인접 리스트(Adjacency List) 방식:
인접 리스트는 각 정점마다 이어지는 간선의 목록을 표현한 것이다. 각각의 정점에 인접한 정점들을 리스트로 표현한 것이다. 이렇게 인접리스트는 배열이나 연결 리스트를 이용해서 표현한다.
일단 모든 정점(Vertex)은 하나의 인접 리스트를 가져서 최소로 차지하는 공간은 O(V)이며 무방향 그래프는 똑같은 간선을 2개씩 저장하기에 2E(edge), 방향 그래프에서는 E의 공간을 사용한다. 합치면 O(V + E)만큼의 공간을 사용한다고 표현한다.

인접 행렬(Adjacency Matrix) 방식:
정점들의 연결관계를 나타내는 2차원 배열
인접 행렬은 V x V 크기의 행렬에 각 정점의 간선 유무 및 가중치에 따라 행렬의 요소를 채워준다.
무방향 그래프는 서로 연결되어 있기에 행렬이 대칭적이다. 하지만 방향그래프는 대칭적이지 않을 수 있다. 만약 간선들에 가중치가 있을 때는 행렬에 0,1 대신 가중치를 저장해주면 된다. 또한 인접 행렬은 인접한 정점들을 찾기 위해서 모든 정점을 순회해야 한다.

=> 정점의 추가와 삭제는 인접 리스트 방식이 효율적이며, 간선의 추가와 삭제가 빈번히 일어나는 경우에는 인접 행렬 방식이 효율적이다.
'📍 CS > Data Structure' 카테고리의 다른 글
| [19JAN, 2021] Stack & Queue 개념정리 (0) | 2021.01.19 |
|---|
